The full article was original posted at Rounding.to
When you are learning or studying math, it is normal that one of the topics includes rounding numbers. However, as you may already know, rounding numbers is a part of our lives. No matter if you’re in the supermarket and want to ensure you have enough cash to pay the bill or when you’re eating with your colleagues and you want to split the bill.
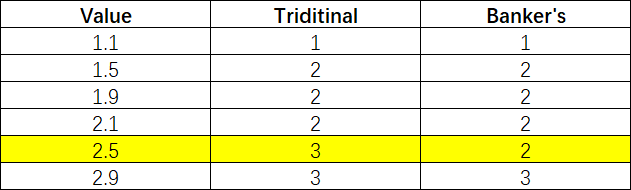
Nevertheless, you may have never heard about Banker’s rounding. So, today, we decided to tell you everything you know about Banker’s rounding process and when you can use it.
What Is Banker’s Rounding
Simply put, Banker’s rounding is an algorithm for rounding quantities to integers. But this algorithm is applied to the numbers that are equidistant from the two nearest integers are rounded to the nearest even integer.
Here are some examples to help you better understand the concept of Banker’s rounding:
0.5 rounds down to 0. Why? Because 0 is the nearest even integer.
1.5 rounds up to 2. Why? Because 2 is the nearest even integer.
73.5 rounds up to 74. Why? Because 74 is the nearest even integer.
74.5 rounds down to 74. Why? Because 74 is the nearest even integer.
75.5 rounds up to 76. Why? Because 76 is the nearest even integer.
76.5 rounds down to 76. Why? Because 76 is the nearest even integer.
These are the most common rounding methods.
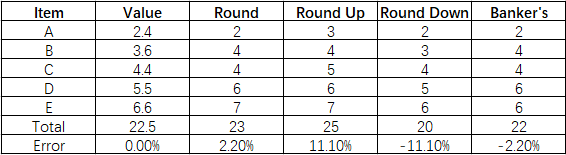
However, when you learn how to round numbers at school, you round the above numbers to the nearest integer the following way:
0.5 rounds up to 1. Why? Because 1 is the nearest integer.
1.5 rounds up to 2. Why? Because 2 is the nearest integer.
73.5 rounds up to 74. Why? Because 74 is the nearest integer.
74.5 rounds up to 75. Why? Because 75 is the nearest integer.
75.5 rounds up to 76. Why? Because 76 is the nearest integer.
76.5 rounds up to 77. Why? Because 77 is the nearest integer.
As you can see, the regular rounding algorithm and the Banker’s rounding deliver different results.
